QUANTIQUE (CHIMIE)

QUANTIQUE (CHIMIE)

L’émergence de la chimie quantique, en temps que domaine de la connaissance scientifique, peut être assez précisément datée: en 1927, W. H. Heitler et F. London proposaient une solution satisfaisante au problème de la stabilisation de la molécule d’hydrogène H². Conjointement avec la détermination de la structure de l’atome d’hydrogène, c’était un argument de poids pour conforter les postulats qui avaient conduit, en 1926, à l’énoncé de l’équation de Schrödinger (cf. E. SCHRÖDINGER). Après des avancées rapides comme l’étude par J. Hylleraas (1929) de l’atome d’hélium ou la détermination précise de la structure de la molécule H² par James et Coolidge (1933), il était possible de souscrire à l’énoncé catégorique de Dirac: «Les lois physiques fondamentales pour une théorie mathématique d’une grande partie de la physique et de toute la chimie sont maintenant complètement connues, et la seule difficulté est que l’application exacte de ces lois conduit à des équations beaucoup trop complexes pour être solubles.» Ce qui était plus difficilement prévisible, c’était que la recherche de solutions approchées et l’analyse de cette équation allaient à la fois accaparer les efforts incessants des chimistes quanticiens et donner naissance à des concepts qui seront très utiles pour interpréter les observations expérimentales.

La chimie quantique, qui cherche à comprendre et à calculer comment interagissent électrons et noyaux, est impliquée dès que des phénomènes physico-chimiques s’expliquent, au niveau microscopique, par des mécanismes quantiques. Les relations, anciennes, avec les autres domaines de la chimie sont de plus en plus fortes, car l’apparition de modèles fiables, accompagnée de logiciels informatiques d’usage commun, a rendu la chimie quantique accessible pour des non-spécialistes. La lecture d’une revue internationale de référence comme Journal of the American Chemical Society montre que plus d’un tiers des articles sont complétés par des considérations théoriques, cela sans prendre en compte les contributions dans lesquelles l’aspect de chimie quantique est primordial.

Le recoupement avec la physique quantique n’a cessé de croître au cours des décennies de 1980 et de 1990. D’une part, la physique quantique a progressivement élargi son champ d’étude à des systèmes de plus en plus complexes et, d’autre part, la chimie quantique, tirant parti de l’amélioration des méthodes d’approximation et des techniques informatiques qui leur sont associées, a su donner des réponses de plus en plus précises aux problèmes structuraux, énergétiques, spectroscopiques posés par l’étude des systèmes avec un petit nombre d’atomes. Elle a également élargi son domaine à des problématiques nouvelles: réponse dynamique d’un système au rayonnement lumineux, évolution d’un système en fonction du temps, etc. La science relativement nouvelle des agrégats (c’est-à-dire les systèmes atomiques homogènes intermédiaires entre la molécule et le solide) est un exemple où la frontière entre les deux disciplines est particulièrement difficile à établir. On peut d’ailleurs considérer que cette partition n’est pas universelle, puisque dans les universités anglo-saxonnes le terme de chemical physics recouvre un domaine dans lequel chimie quantique et physique quantique moléculaire sont parfaitement bien intégrées.

À l’autre extrême, l’interaction avec l’étude des systèmes complexes (macromolécules biologiques, polymères, etc.) a progressivement changé de nature. Après une première période marquée par des recherches de corrélations entre structure moléculaire et activité biochimique (B. et A. Pullman, 1963) et des modélisations semi-empiriques des conformations des macromolécules, il est apparu qu’un traitement directement quantique des problèmes biochimiques et biologiques était hors de portée. Les travaux de M. Karplus et son école (M. Karplus et J. A. McCammon, 1986) ont suscité des approches classiques des problèmes structuraux et dynamiques de ces composés en faisant appel à des champs de force de la mécanique moléculaire. La chimie quantique, en tant que telle, apparaît alors comme une étape intermédiaire pour définir, préciser ou valider les expressions de ces champs de force. Son rôle reste cependant central pour la compréhension des aspects purement quantiques (transferts électroniques, photosynthèse, réactivité des sites actifs des enzymes, etc.) où la complexité des systèmes pose des problèmes spécifiques.

Définir des méthodes approchées de résolution de l’équation de Schrödinger, appliquer ces méthodes à des molécules d’intérêt chimique, biochimique, astrochimique, etc., pourrait faire penser à une activité essentiellement technique, où les principales avancées seraient liées soit à des progrès dans l’utilisation des mathématiques appliquées et de l’analyse numérique, soit à un meilleur profit tiré des ressources informatiques. Ces aspects sont très importants dans l’évolution de la discipline et jouent un rôle central dans la qualité grandissante des résultats. Parallèlement à ce travail, la chimie quantique a su produire des concepts nouveaux, soit pour rationaliser et quantifier des notions plus anciennes proposées par les chimistes expérimentateurs (comme ceux de liaison chimique, d’aromaticité, de résonance, de basicité et d’acidité, etc.), soit pour éclairer son propre champ d’investigation (énergie de corrélation, orbitales moléculaires, localisation versus délocalisation, excitations moléculaires).

1. États stationnaires, approximation de Born-Oppenheimer

Dans sa formulation non relativiste, le hamiltonien (cf. mécanique QUANTIQUE) associé à un système isolé formé par N noyaux (de masses m size=1^猪 , de charges Z size=1^猪 et positions ぱ size=1^猪) et n électrons (repérés par les coordonnées るⁱ ) s’écrit:

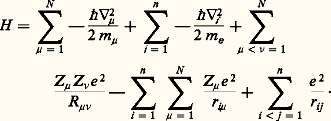Les deux premiers termes représentent respectivement les opérateurs associés aux énergies cinétiques des noyaux et des électrons, et les trois termes suivants, les opérateurs associés aux interactions électrostatiques entre noyaux, entre noyaux et électrons et entre électrons eux-mêmes.

L’équation de Schrödinger associée:

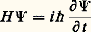détermine la fonction d’onde 切( ぱ size=1^猪, るⁱ , t ) à partir de laquelle toutes les propriétés du système peuvent être déduites.

L’expression de H indique que, dans la plupart des cas, il n’existe pas de solution analytique exacte de cette équation. Les deux seules exceptions à cette règle sont le système avec un électron dans un potentiel central (c’est-à-dire l’atome d’hydrogène et les atomes hydrogénoïdes analogues) et celui qui est composé par un électron dans le champ créé par deux noyaux (comme par exemple H⁺²). On mesure ainsi les difficultés rencontrées pour obtenir une approximation fiable de 切 pour un système d’une dizaine d’atomes et de quelques dizaines d’électrons, problème qui constitue le cœur des applications de la chimie quantique. C’est seulement en combinant les données de la chimie, les considérations physiques sur le type, la localisation, la force des interactions et les méthodes mathématiques adaptées que ce but peut être atteint.

La chimie quantique est surtout concentrée sur la recherche d’états stationnaires, associés à des énergies définies, qui sont solutions de l’équation indépendante du temps H 祥 = E 祥, où 祥 ne dépend plus que des variables ぱ size=1^猪 et るⁱ . Il existe cependant toute une classe de phénomènes qui font intervenir explicitement l’évolution en fonction du temps, comme par exemple le passage d’un état stationnaire à un autre état stationnaire sous l’effet du rayonnement ou l’évolution temporelle au cours d’une réaction chimique. La solution de ces problèmes fait appel à des méthodes spécifiques dont l’exposé dépasse le cadre de cette contribution (cf. D. G. Truhlar, 1994).

La seconde étape vers une simplification du problème requiert une approximation pour séparer le mouvement des noyaux de celui des électrons. La justification physique est fondée sur la différence de masse (donc de vitesse) entre noyaux et électrons. L’approximation de Born-Oppenheimer suppose que, pour chaque position ぱ size=1^猪 des noyaux, le mouvement des électrons est suffisamment rapide pour que la solution obtenue en supposant les noyaux fixes soit proche de la solution exacte. Elle introduit le hamiltonien électronique H^e , qui correspond aux mouvements des électrons dans le champ des noyaux fixes et dont la solution ne dépend que des coordonnées des électrons. Ainsi se met en place la notion très importante de surface de potentiel : il s’agit de la fonction E^e ぱ size=1^猪, qui associe l’énergie électronique à chaque position des noyaux et qui joue le rôle d’énergie potentielle pour leurs mouvements. L’exploration de cette surface donne des informations fondamentales sur la structure moléculaire: aux minimums locaux sont associés les différents isomères stables possibles, et le passage par les cols correspond aux états de transition entre les isomères ou entre réactifs et produits d’une réaction chimique. Les données énergétiques fondamentales (énergie de dissociation d’une liaison, enthalpie de réaction, etc.) peuvent être obtenues à partir de cette surface.

Malgré ces simplifications, l’équation reste complexe: c’est une équation aux dérivées partielles du second ordre portant sur 3 n variables et il faut faire d’autres approximations portant sur la forme même de 祥 るⁱ.

2. Modèle «valence bond», ou modèle de paires

Historiquement, le modèle de paires est le modèle utilisé par W. H. Heitler et F. London et il fait largement appel à l’intuition chimique à propos de la formation des liaisons. Dans le cas simple de H², la fonction d’onde de départ est constituée par le produit 﨏^A(r ^1A) 﨏^B(r ^2B) des deux solutions correspondant aux atomes d’hydrogène A et B sans interaction. La stabilisation (faible puisque l’énergie de liaison obtenue est 24 kJ 練 mol size=1^漣1 au lieu de 455 kJ 練 mol size=1^漣1 expérimentalement) est due à l’énergie électrostatique. Lorsque la distance entre les noyaux est réduite, il n’est plus possible de distinguer entre les deux électrons, et une solution plus satisfaisante de la fonction est alors 﨏^A(r ^1A) 﨏^B(r ^2B) + 﨏^B(r ^1B) 﨏^A(r ^2A). L’énergie de liaison calculée est alors beaucoup plus forte (303 kJ 練 mol size=1^漣1), et c’est la contribution d’échange qui apporte la contribution principale. La description par Lewis de l’origine de la liaison chimique par formation d’une paire d’électrons est donc confirmée. Si l’on affine le traitement en admettant que les fonctions 﨏^A et 﨏^B ne sont plus les mieux adaptées lorsque la distance décroît et qu’on autorise leur déformation, on obtient une énergie de liaison de 363 kJ 練 mol size=1^漣1. La dernière amélioration, introduisant d’autres répartitions des électrons (formes de valence), par exemple celles où les deux électrons sont liés au même atome, porte en germe les limites de la méthode: dans un cas complexe, le nombre de formes de valence possibles sera très grand et le processus de choix des formes nécessaires, fondé sur l’image de la description chimique du système n’est pas simple. Le modèle valence bond a donc subi, malgré ses qualités intrinsèques, une longue période d’éclipse avant de connaître un regain d’intérêt en tant que méthode quantitative d’étude.

3. Orbitales moléculaires

Modèle à particules indépendantes

La plus grande difficulté rencontrée pour résoudre l’équation de Schrödinger est l’existence des termes de répulsion coulombienne 1/r^ij , qui couplent les mouvements des électrons. Pour satisfaire au principe d’antisymétrie de Pauli (cf. mécanique QUANTIQUE), Slater a proposé de chercher une fonction approchée sous la forme d’un déterminant bâti sur des fonctions 﨏ⁱ (les orbitales moléculaires) dépendant des coordonnées d’espace et de spin d’un seul électron:

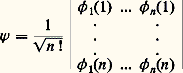Pour déterminer les fonctions 﨏ⁱ , on fait appel au principe variationnel qui établit que si E ⁰ est la plus basse valeur propre d’un opérateur hamiltonien H , alors pour toute fonction 祥 on a l’inégalité:

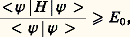l’égalité n’étant vérifiée que si 祥 est la fonction propre associée à E ⁰. Dans le cas présent, l’espace des fonctions 祥 est restreint, puisqu’il ne comprend que les fonctions qui s’écrivent comme un déterminant de Slater et le principe variationnel ne permet pas d’atteindre la valeur exacte E ⁰, mais une approximation dite énergie limite Hartree-Fock: E ^HF 礪 E ⁰.

La mise en œuvre du principe variationnel est trop longue pour être développée ici (cf. A. Szabo et N. Ostlund, chap. III, 1982) et nous rappellerons seulement la démarche suivie. En utilisant l’expression du déterminant de Slater, l’énergie associée E se décompose comme une somme d’intégrales à un ou deux électrons impliquant les opérateurs composant H . Le principe variationnel appliqué à E , par rapport aux variations des orbitales 﨏ⁱ , conduit à n équations:

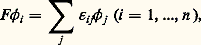où les 﨎^ij sont les multiplicateurs de Lagrange associés aux contraintes d’orthogonalité entre les orbitales 﨏ⁱ et où F , opérateur de Fock, est défini par:

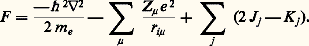Les deux premiers termes représentent la partie cinétique et l’interaction d’un électron avec les noyaux et les deux derniers l’interaction d’un électron avec l’ensemble des autres électrons. Ces équations sont connues sous le nom d’équations de Hartree-Fock et elles sont à la base de la plupart des études ab initio de chimie quantique. Il est possible de réécrire les équations de Hartree-Fock sous forme diagonale, F 﨏ⁱ = 﨎ⁱ 﨏ⁱ , et ces solutions particulières 﨏ⁱ (appelées orbitales canoniques) ont les mêmes propriétés de symétrie que H , ce qui implique leur délocalisation. Elles sont également bien adaptées pour interpréter de façon simple des propriétés élémentaires des molécules, comme le potentiel d’ionisation (théorème de Koopmans) ou les propriétés spectroscopiques en termes d’excitations élémentaires. Elles jouent aussi un rôle central dans l’interprétation de la réactivité chimique en terme d’orbitales frontières (cf. K. Fukui, 1964). Ces caractéristiques, très utilisées pour rationaliser la structure électronique des molécules, peuvent conduire à une «survalorisation» de ce concept d’orbitales moléculaires qui n’a pas de réalité physique mais qui résulte du choix d’une approximation pour la fonction d’onde et d’une base particulière de fonctions à une particule. D’autres bases de fonctions, où les orbitales moléculaires sont localisées, correspondent mieux à la description de Lewis de la structure électronique, avec des paires d’électrons mises en commun pour former les liaisons covalentes.

La résolution des équations de Hartree-Fock est complexe, puisqu’il s’agit d’équations aux dérivées partielles d’ordre 2 portant sur les trois coordonnées de l’électron et que F dépend des solutions cherchées (d’où la nécessité d’une solution itérative). Sauf pour les atomes, il n’existe pas de solution numérique directe: on introduit une base de fonctions fixes 﨑^p et la résolution des équations de Hartree-Fock est alors remplacée par la détermination des coefficients C^ip tels que:

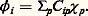Ce processus, formalisé par C. C. J. Roothaan (1951), aboutit à l’équation matricielle: FC = SC 﨎, où C et 﨎 sont les coefficients et les énergies des orbitales moléculaires cherchées et F et S les expressions matricielles des opérateurs F et de recouvrement dans la base 﨑^p. Guidé par l’idée que chaque atome garde partiellement son identité dans la molécule, on choisit en général comme base 﨑^p des fonctions centrées sur les différents atomes de la molécule (d’où le nom de linear combination of atomic orbitals ) et, depuis les travaux de Boys, la plupart des programmes de calcul ab initio utilisent comme orbitales 﨑^p des fonctions gaussiennes cartésiennes. Les efforts très importants consacrés à la mise en place de techniques numériques efficaces pour le calcul des éléments de F et au choix judicieux des orbitales 﨑^p ont permis d’obtenir des solutions précises du problème de Hartree-Fock pour des molécules de grande taille (Bénard et coll., 1994).

Les nombreuses discussions sur la qualité de la fonction 祥^HF et des observables associés ont permis de dégager des tendances générales: géométrie et stabilité des différents isomères en bon accord avec l’expérience, fréquences de vibration du mouvement des noyaux surestimées d’environ 10 p. 100, densité électronique proche de la densité exacte (ce qui permet de faire des analyses fiables de la distribution de charges). En revanche, les insuffisances sont suffisamment claires (énergies de liaison très fortement sous-estimées, difficultés pour décrire les liaisons inhabituelles comme les liaisons hypervalentes ou multiples, divergence lorsqu’il y a rupture d’une liaison, impossibilité de décrire des états électroniquement excités) pour qu’il ait été nécessaire de dépasser ce stade dans de nombreux cas.

Méthodes post-Hartree-Fock

Le modèle à particules indépendantes, qui conduit aux équations de Hartree-Fock, ne tient compte de l’interaction entre électrons que de façon moyenne, mais il permet de définir un ensemble d’orbitales moléculaires 﨏ⁱ dont un sous-ensemble seulement est utilisé pour construire le déterminant de Slater 祥^HF. Dans la plupart des cas, pour dépasser cette approximation, la fonction 祥 est développée comme une combinaison linéaire de configurations 祥^k où chaque 祥^k est caractérisée par des couples d’indices (r , s ), (t , u ), ..., qui repèrent quelles sont les orbitales 﨏^r , 﨏^t , ..., occupées dans 祥^HF, qui sont, dans 祥^k remplacées par 﨏^s , 﨏^u , ...:

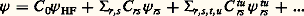L’utilisation de l’ensemble complet des configurations 祥 ^k , qui donnerait la meilleure solution possible (dans la base des fonctions monoélectroniques de départ), est impossible dans la plupart des cas réels, puisque le nombre de configurations croît exponentiellement avec le nombre d’électrons du système. Le mode de détermination des coefficients Cⁱ (par application du principe variationnel, par un développement de type perturbatif ou par une expansion de type «cluster»), le choix de l’ensemble des configurations inclues dans le développement et la définition des fonctions de base 﨏ⁱ donnent lieu à une très grande diversité de méthodes dont le développement s’est fait en relation étroite avec d’autres domaines de la physique où ce problème du mouvement corrélé de n -corps est également posé. C’est aussi un aspect de la chimie quantique où les dernières avancées ont été étroitement liées à l’évolution des moyens informatiques. Malgré des succès remarqués, par exemple dans l’étude des états excités, la convergence de ces approches (par rapport au nombre de configurations et de fonctions 﨏ⁱ ) est généralement lente.

Depuis les travaux de James et Coolidge, la contribution importante des termes dépendant directement de r ^ij dans l’expression de 祥 a été reconnue et d’autres travaux (Kutzelnigg et coll., 1991) ont démontré que des solutions existent pour introduire ces termes de façon générale même si les calculs sont plus complexes qu’avec les approches standards. Signalons également que les approches dites Monte-Carlo quantiques, s’affranchissant des contraintes de base et de développement de configurations, ont donné les résultats les plus précis pour les systèmes de petite taille.

4. Fonctionnelle de la densité

En 1964, P. Hohenberg et W. Kohn énonçaient un théorème qui ouvrait une voie nouvelle: pour tout système, l’énergie associée à un état fondamental non dégénéré est une fonctionnelle unique de la densité électronique E = G [ 福( る)] et la densité électronique 福 exacte correspond au minimum de E . Si le principe variationnel est appliqué (W. Kohn et L. J. Sham, 1965) à la détermination des fonctions 﨏ⁱ telles que:

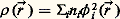(n ⁱ est le nombre d’électrons dans l’orbitale 﨏ⁱ ), celles-ci sont solutions d’équations formellement analogues aux équations de Hartree-Fock:

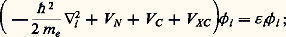V^N et V^C , qui correspondent aux interactions coulombiennes avec les noyaux et les électrons respectivement, sont définis sans ambiguïté à partir de l’expression de l’énergie totale. Le choix du terme V^XC , qui contient les contributions d’échange et de corrélation, est beaucoup plus délicat en l’absence d’une dérivation exacte de la fonctionnelle G . La solution la plus couramment employée consiste à écrire V^XC comme une fonction locale de la densité 福, déterminée dans le cas limite d’un gaz homogène d’électrons pour lequel des valeurs exactes de E en fonction de 福 peuvent être calculées. D’autres formes de V^XC [ 福] existent, introduisant par exemple le gradient de 福 pour tenir compte de l’inhomogénéité de la densité. Après quelques années pendant lesquelles les applications à des systèmes moléculaires donnaient des résultats de «qualité imprévisible», cette approche s’est imposée comme une alternative efficace aux méthodes ab initio traditionnelles. Le débat sur les fondements, sur la recherche des meilleures formes fonctionnelles de V^XC [ 福], sur les extensions aux états excités est très ouvert et très actif.

R. Car et M. Parinello (1985) ont proposé d’utiliser cette formulation du problème électronique pour traiter simultanément le mouvement (classique) des noyaux et la détermination (quantique) de la densité électronique. Cette démarche, qui peut être utilisée dans d’autres cadres, semble extrêmement puissante pour déterminer la structure et la stabilité de systèmes complexes, puisqu’elle dispense de déterminer, pour chaque position des noyaux, l’expression de la fonction d’onde.

5. Les méthodes semi-empiriques

Ces approches ont joué un rôle historiquement très important dans le développement de la chimie quantique. Certaines d’entre elles sont encore abondamment utilisées pour les applications à la chimie et aux systèmes infinis. Elles correspondent à différents niveaux de simplifications de H et le qualificatif «semi-empirique» vient du fait que certains éléments de matrice de H simplifié sont ajustés sur des données expérimentales.

Méthode de Hückel

La méthode de Hückel est la plus ancienne (1931) et la plus simple des méthodes semi-empiriques. Le hamiltonien ne contient que des termes monoélectroniques:

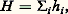où la forme de hⁱ n’est pas explicitement précisée et, dans sa forme originale, elle ne s’applique qu’à l’étude du système des électrons 神. L’énergie E size=1^神 est calculée comme

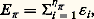(n size=1^神 est le nombre d’orbitales 神 occupées et 﨎ⁱ est la valeur propre de h ⁱ 﨏ⁱ = 﨎ⁱ 﨏ⁱ ). La version la plus simple de la méthode de Hückel ne retient dans la construction de la matrice de H que deux types de termes: les termes diagonaux, caractéristiques de l’atome, et les termes entre deux atomes chimiquement liés. L’expression de l’énergie électronique obtenue met en évidence plusieurs facteurs importants dans l’explication de la nature de la liaison chimique: la stabilisation de l’énergie est liée à la valeur de l’intégrale de transfert 廓 entre deux atomes voisins et la localisation des orbitales correspondantes reflète la différence des potentiels d’ionisation. La méthode de Hückel a permis de proposer des explications rationnelles à plusieurs observations expérimentales au sujet des hydrocarbures insaturés (importance de l’énergie de délocalisation, stabilisation des cycles comportant 4 n + 2 atomes, déstabilisation des cycles avec 4 n atomes ^{[cf. AROMATICITÉ]}, effets pseudo-Jahn-Teller, évolution des transitions électroniques, etc.). Dans le même esprit, Woodward et Hoffman ont introduit la méthode dite de «Hückel étendue» (E.H.T.) dans laquelle le hamiltonien monoélectronique fait intervenir l’ensemble des électrons de valence de la molécule. Les éléments non diagonaux sont calculés par une formule qui fait intervenir les éléments diagonaux des deux atomes concernés et l’intégrale de recouvrement. La méthode E.H.T. a remporté de grands succès: elle a servi en particulier de fondement théorique aux règles de Woodward et Hoffman (1965) prédisant, à partir de propriétés de symétrie des orbitales moléculaires, la faisabilité de plusieurs classes de réactions chimiques et elle a permis une description, au moins qualitative, de très nombreux complexes organométalliques.

Méthodes Hartree-Fock simplifiées

Dans le but de simplifier la solution des équations de Hartree-Fock, il est possible de négliger certaines intégrales qui sont faibles en valeur relative. Les méthodes Z.D.O. (zero differential overlap ) ont un point de départ commun: supposer que tout ou partie des intégrales de recouvrement sont nulles, ce qui entraîne la réduction du nombre des intégrales biélectroniques nécessaires pour trouver une solution 祥^HF approchée. Cette simplification est compensée par l’introduction de paramètres adaptés pour reproduire, sur une série de composés de la même famille, un ensemble de données physico-chimiques. Par rapport à l’approximation de Hückel, les méthodes Z.D.O. présentent l’avantage de donner une expression approchée mais physiquement fondée de l’énergie totale et donc de permettre des études de structure ou de mécanismes de réaction. Elles donnent des résultats qui se comparent souvent avantageusement à ceux des méthodes ab initio , pour un coût bien moindre, mais leur champ d’application est toujours limité par les caractéristiques des molécules formant la famille qui a servi à dériver les paramètres (J. A. Pople et D. Beveridge, 1970).

6. Interactions moléculaires

Si l’on place à part, dans l’ensemble des problèmes abordés par la chimie quantique, l’étude des forces intermoléculaires – ou forces de Van der Waals-London –, c’est parce qu’elles font intervenir des énergies nettement plus faibles (de 10 à 40 kJ 練 mol size=1^漣1) que dans le cas des liaisons chimiques ordinaires. Ces interactions jouent cependant un rôle fondamental dans la compréhension des phénomènes physico-chimiques impliquant un système moléculaire en interaction avec un environnement (molécule en solution, molécule dans une matrice solide, agrégats moléculaires), et la modélisation semi-empirique de ces interactions tient une place importante dans les développements de la chimie quantique appliquée aux systèmes complexes.

Soit deux molécules A et B, situées dans l’espace à une distance R ^AB. L’énergie d’interaction E (R ^AB) est la différence entre l’énergie du complexe E ^AB(R ^AB) et la somme des énergies des systèmes isolés E ^A et E ^B:

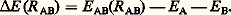La première approche consiste à calculer de la façon la plus précise possible les différents termes E ^AB(R ^AB), E ^A et E ^B et utiliser simplement l’équation précédente. Cette méthode de la supermolécule présente l’avantage évident de ne pas nécessiter la mise en œuvre d’une méthodologie particulière, puisque le calcul de E ^AB(R ^AB), E ^A et E ^B sera conduit avec le même type d’approximation. Cependant, comme E (R ^AB) est une quantité très petite calculée comme la différence entre des énergies beaucoup plus fortes, cette voie devient impraticable dès que la taille des molécules en interaction est supérieure à quelques atomes (N 麗 10 atomes).

La seconde approche cherche, en revanche, à tirer parti de la petitesse de l’interaction moléculaire pour la considérer comme une perturbation par rapport à la somme des hamiltoniens H ^A et H ^B des systèmes séparés. L’hamiltonien total H ^AB est donc réécrit comme H ^AB = H ^A + H ^B + 益^AB, où 益^AB regroupe tous les termes qui font intervenir les interactions entre noyaux et électrons de A et de B.

Ce développement de perturbation devrait donner directement une expression de E ^AB(R ^AB) en fonction de 益^AB et des fonctions propres de H ^A et H ^B, mais, comme nous l’avons vu, dans le cas général, les solutions exactes de H ^A et H ^B sont inconnues. Si l’on écrit le développement par rapport à des solutions approchées (par exemple Hartree-Fock) des sous-systèmes, l’expression E ^AB(R ^AB) contient des termes dont l’origine n’est pas strictement intermoléculaire et qui contribuent à l’énergie des sous-systèmes isolés. Cette limitation complique l’analyse de la série de perturbation et en ralentit la convergence. En fait, sauf dans le cas de l’interaction de petits systèmes, l’utilisation des méthodes de perturbation est plus complexe que celle de l’approche supermolécule et elle nécessite le développement de logiciels spécifiques. Son avantage principal réside dans l’interprétation physique claire que l’on peut donner aux différents termes qui apparaissent, aux premiers ordres de perturbation, c’est-à-dire:

– l’énergie de répulsion liée au recouvrement entre les nuages électroniques;

– les interactions entre les distributions électrostatiques (énergie coulombienne et de polarisation);

– les transferts d’électrons d’un système à l’autre (énergie de délocalisation);

– les interactions entre fluctuations instantanées des distributions de charge (énergie de dispersion ou de London).

L’importance relative des différents termes dépend à la fois de la distance entre les deux systèmes et de leurs caractéristiques électrostatiques. Leur étude permet la définition de formes analytiques pour représenter les différents termes, ainsi que l’ajustement des paramètres qui apparaissent dans ces formes analytiques. L’expression la plus ancienne, due à Lennard-Jones, ne retient que les termes de répulsion et de dispersion, sous la forme

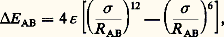où le minimum de la courbe d’interaction se situe à R ⁰ = (2)^1/6 靖 pour une interaction égale à 﨎. Ce type de potentiel est utilisé pour représenter l’interaction entre des systèmes de symétrie sphérique, sans charge nette ni moment multipolaire aux bas ordres, par exemple les interactions entre atomes de gaz rare. Il a joué, par sa simplicité et son efficacité pour le calcul numérique, un rôle essentiel dans les premières tentatives de simulation d’ensembles moléculaires ou atomiques de type Van der Waals par les méthodes de dynamique moléculaire.

Pour des systèmes moléculaires polyatomiques, il faut introduire des développements pour les différents termes (P. Claverie, 1982): développements multipolaires ou répartition de charges ponctuelles pour la contribution électrostatique, introduction des polarisabilités atomiques ou de liaisons pour les contributions d’induction et dispersion, etc.

Malgré le très grand nombre d’études théoriques, ab initio ou semi-empiriques, consacrées à ce sujet, il n’y a pas encore de véritable consensus sur le choix des potentiels intermoléculaires. Sur un système apparemment simple comme l’eau, les différents potentiels proposés ont tous montré des déficiences nettes lorsqu’ils sont utilisés pour reproduire les propriétés thermodynamiques dans une large gamme de température et de pression. La précision de ces potentiels intermoléculaires est aussi un point central pour l’application des méthodes de simulation numérique au comportement des macromolécules et des polymères, où, sous le nom d’interactions non liées, elles jouent un rôle clé dans la détermination des conformations de ces systèmes. Les interactions moléculaires entre systèmes dans un état électroniquement excité sont encore mal comprises et difficilement modélisables.

7. Orientations actuelles

Le champ d’application des méthodes de la chimie quantique s’est considérablement élargi au cours des décennies de 1980 et de 1990. À un domaine traditionnel, centré principalement autour des applications à la chimie organique, sont venus s’ajouter, ainsi que nous l’avons vu, des interactions fortes avec d’autres aspects de la chimie, de la physique, de la biologie, de l’astrophysique, etc. La compréhension microscopique détaillée de la structure des atomes, des molécules, des agrégats, des systèmes étendus est un pas très important pour appréhender l’ensemble de leurs propriétés physico-chimiques (même si d’autres approches plus macroscopiques ont elles aussi démontré leur pertinence). Cette évolution a inévitablement engendré une tension et un éclatement dans une discipline qui avait gardé pendant plusieurs décennies une certaine unité. En effet, les moyens à mettre en œuvre et les résultats à attendre d’une étude quantique d’une molécule d’intérêt biochimique ou d’un complexe organométallique n’ont que peu à voir avec ceux qui sont relatifs à une étude spectroscopique très précise d’une molécule diatomique. La mise à disposition de logiciels de plus en plus efficaces et de plus en plus faciles à utiliser comporte des avantages, mais elle contribue également à obscurcir la perception que des non-spécialistes pensent avoir de la discipline. Le choix de la méthode et du logiciel adaptés, et une estimation raisonnable de la qualité des résultats, restent encore une matière difficile. Le premier défi que rencontre la discipline est donc d’assurer une organisation des concepts et une transmission du savoir qui soient plus facilement accessibles à l’ensemble de la communauté scientifique concernée.

En ce qui concerne les études structurales des molécules et des agrégats (géométries, réactivité), les avancées ont été considérables au cours des dernières années, et cela dans plusieurs directions. Le traitement des effets relativistes, l’utilisation de pseudopotentiels pour les électrons de cœur ont permis d’étendre à l’ensemble du tableau périodique le domaine des études ab initio , mais certains composés continuent à poser des problèmes complexes. Les métaux de transition, en raison de l’occupation partielle de la couche nd et des contributions très importantes de la corrélation, n’ont pas encore livré tous leurs secrets. L’échec lancinant des méthodes ab initio les plus élaborées pour reproduire, ne serait-ce qu’approximativement, les caractéristiques d’une liaison multiple comme celle de Cr ² signifie clairement que les approches traditionnelles du traitement de la corrélation électronique sont insuffisantes.

La théorie de la fonctionnelle de la densité a remporté d’incontestables succès, puisqu’elle permet de prendre en compte, à moindre frais, les effets de corrélation. Après des années pendant lesquelles les qualités intrinsèques de la méthode ont été masquées par une mise en œuvre rudimentaire, les résultats récents l’ont placée dans une situation favorable par rapport aux approches traditionnelles. La recherche d’une forme de fonctionnelle de l’énergie mieux adaptée aux systèmes électroniques inhomogènes et la possibilité de traiter de façon générale des états électroniques excités sont également des défis que la discipline devra affronter dans les années à venir.

Quelle que soit la méthode utilisée pour calculer l’énergie électronique, la surface de potentiel associée aux mouvements des noyaux pour un système complexe (macromolécule, agrégat) présente des caractéristiques qui en rendent la représentation analytique et l’exploration extrêmement difficiles. Même si la présentation des méthodes utilisées (statistiques comme les méthodes de Monte-Carlo ou fondées sur la dynamique classique) sort du cadre strict de la chimie quantique, il est évident que cette difficulté doit être prise en compte avant d’envisager l’étude de ces systèmes complexes. Des approches mixtes, où sont traités simultanément le mouvement (classique) des noyaux et l’optimisation de la fonction électronique (quantique) apparaissent comme très prometteuses, malgré des difficultés de fond (R. Car et M. Parinello, 1985).

La chimie quantique a su se doter de méthodes puissantes d’approximation de l’équation de Schrödinger. Le chemin parcouru peut être mesuré en relisant le commentaire pessimiste de Kauzmann dans son manuel de 1957: «Malheureusement, la chimie quantique n’a pas eu beaucoup de succès pour résoudre des problèmes de ce type (par exemple le calcul de l’énergie de dissociation). À proprement parler, il y a eu quelques progrès dans le développement de méthodes d’interpolations approchées grâce auxquelles certaines propriétés des molécules peuvent être déduites à partir des propriétés d’autres molécules [...]. Cependant, ces méthodes sont fondées sur des approximations grossières, qui semblent avoir tendance à devenir gravement fausses sans raison apparente.» La situation actuelle est bien différente, comme en témoigne la publication de compilations de résultats structuraux obtenus par des études de chimie quantique sur des ensembles de composés, connus ou non, résultats qui «seront de qualité suffisante ou pourront être utilisés comme point de départ pour des études expérimentales plus fines» (F. Hampel, 1994). Même si l’heure n’est pas venue où la simple lecture d’une formule permettra de préciser les propriétés de la molécule qu’elle représente (cf. chimie ORGANIQUE), les progrès de la discipline ont permis de franchir un pas important dans cette voie.

Encyclopédie Universelle. 2012.